1 Formulas
Here a few formulas:
![]()
Seien ![]() ein endlichdimensionaler Euklidischer Vektorraum, sei
ein endlichdimensionaler Euklidischer Vektorraum, sei ![]() orthogonal. Dann existiert eine ONB
orthogonal. Dann existiert eine ONB ![]() von
von ![]() , sodass
, sodass
![Rendered by QuickLaTeX.com \begin{aligned}[][T]_{\mathcal {B}}=\left (\begin{matrix}D_{1} & & 0 \\ & \ddots & \\ 0 & & D_{m}\end{matrix}\right ),\end{aligned}](https://zuugs.ch/showcase/formeln/wp-content/ql-cache/quicklatex.com-f90da3825dded24efc0ffef5c01d0ad3_l3.png)
wobei ![]() oder von der Form
oder von der Form ![]() mit
mit ![]() und
und ![]() ist. Falls
ist. Falls ![]() , dann kann man alle
, dann kann man alle ![]() Blockdiagonaleinträge gleich
Blockdiagonaleinträge gleich ![]() wählen.
wählen.
How to
The formulas are added with the latex-shortcode in Zuugs,
![]()
and there are more advanced functionalities for the initiated.
At first, we sample ![]() in the
in the ![]() (
(![]() is odd) equidistant points around
is odd) equidistant points around ![]() :
:
![]()
where ![]() is some step.
is some step.
Then we interpolate points ![]() by polynomial
by polynomial
(1) 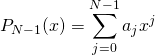
Its coefficients ![]() are found as a solution of system of linear equations:
are found as a solution of system of linear equations:
(2) ![]()
References to existing equations are below.
Here are references to existing equations: (1), (2).